Constructing a Game Graph

This example demonstrates how to construct a simple game on graph. There are three ways to define a game on graph, namely

• By explicitly adding vertices and edges to the graph and marking the accepting states,
• By providing a transition system and a formal specification,
• By providing a game field and player objects.

Note

IGLSynth v0.2.2 only supports explicit construction of graph.

Define Game by Explicit Construction

The module iglsynth.game.game provides necessary classes to define a game on graph. Hence, first import the game.game module:

from iglsynth.game.game import Game

Note that Game class defines a deterministic two-player zero-sum game on graph.

A Game can be either TURN_BASED or CONCURRENT. For this example, let us consider a TURN_BASED game on graph shown in following image.

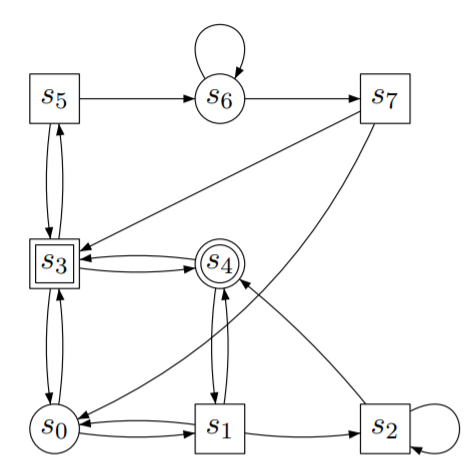
First, instantiate a game object:

game = Game(kind=TURN_BASED)

Now, add the vertices and assign each vertex to a player. When a vertex has turn = 1, player 1 (circle) will make a move. When a vertex has turn = 2, player 2 (box) will make a move.

The vertex in a game (an instance of Game class) must be of type Game.Vertex or its derivative. Hence, it is recommended to instantiate a new game vertex as game.Vertex:

vertices = list()
for i in range(8):
    if i in [0, 4, 6]:
        vertices.append(game.Vertex(name=str(i), turn=1))
    else:
        vertices.append(game.Vertex(name=str(i), turn=2))

game.add_vertices(vertices)

and mark the vertices 3, 4 as final:

# Set the states as final
v3 = vertices[3]
v4 = vertices[4]
game.mark_final(v3)
game.mark_final(v4)

Finally, add the edges to the game. Similar to vertices, we instantiate new edges as game.Edge objects:

# Add edges to the game graph
edge_list = [(0, 1), (0, 3), (1, 0), (1, 2), (1, 4), (2, 4), (2, 2), (3, 0), (3, 4), (3, 5), (4, 3),
             (5, 3), (5, 6), (6, 6), (6, 7), (7, 0), (7, 3)]

for uid, vid in edge_list:
    u = vertices[uid]
    v = vertices[vid]
    game.add_edge(game.Edge(u=u, v=v))

Now, given a game we invoke the ZielonkaSolver from iglsynth.solver.zielonka module to compute the winning regions for players 1 and 2:

from iglsynth.solver.zielonka import ZielonkaSolver
solver = ZielonkaSolver(game)
solver.solve()

The solver.solve() runs the solver on the Game object game that encodes the game on graph. The solution of solver can be accessed using the properties:

print(solver.p1_win)
print(solver.p2_win)

which returns the winning sets for P1 and P2.